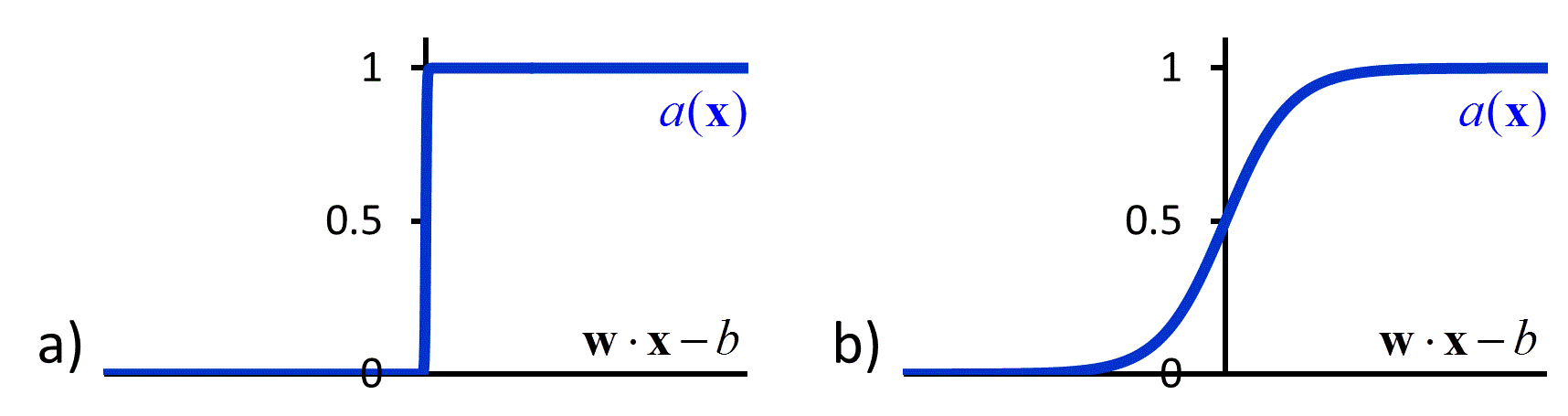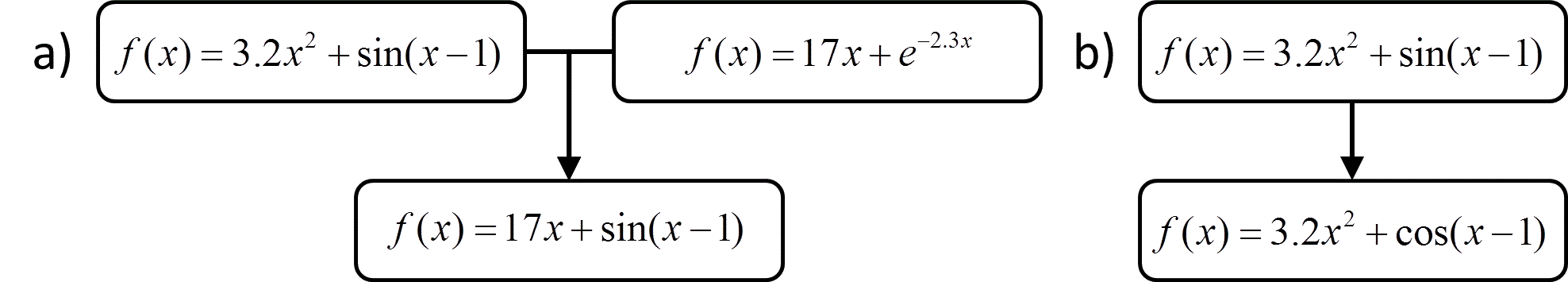A version of this tutorial has been included as a section in the following book chapter:

I would like to thank my co-authors and editors, as well as Hariharan Iyer and David LaVan at NIST, for their valuable comments and assistance in editing this text. I would also like to thank Alberto Hernandez-Valle for converting this material to HTML. This work was supported by the National Science Foundation under grant DMR-1352373. If you find this tutorial useful, please cite the above chapter. If you have any feedback, please let me know.
1.5. Estimating the Prediction Error
2. Supervised Learning Algorithms
2.1. Regularized Least Squares
2.3.1. Reproducing Kernel Hilbert Spaces
One of the fundamental goals of science is the development of theories that can be used to make accurate predictions. Predictive theories are generated through the scientific method, in which existing knowledge is used to formulate hypotheses, which are then used to make predictions that can be empirically tested with the goal of identifying the hypotheses that make the most accurate predictions. The scientific method can be expressed mathematically by considering predictive theory as a function f that maps a set of input data x to a predicted outcome y. The function may be relatively simple, as in Newton’s laws of motion, or it may be complex, as in models that predict the weather based on meteorological observations. The collection of known input (x) and output (y) values, called training data, may be generated through observations or controlled experiments. The goal of the scientist is to use such training data, as well as any other prior knowledge, to identify a function that is able to predict the output value for a new set of input data accurately. The process of identifying such a function from a set of known x and y values is called supervised learning. If the allowed output values y form a continuous range (e.g., melting points), then the process of searching for a function is known as regression. If the allowed output values form a discrete set (e.g., space groups), the process is then known as classification.
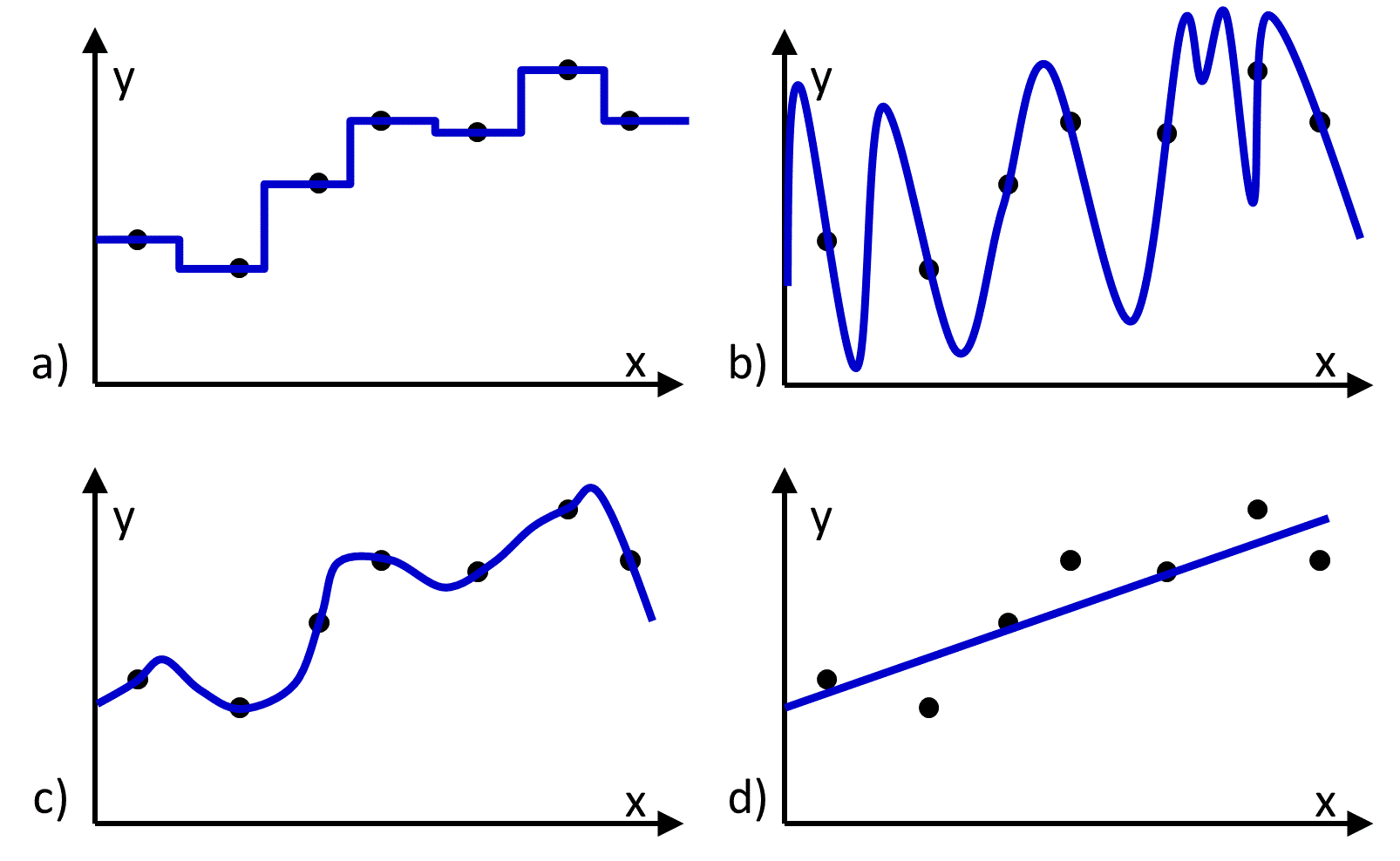
Figure 1 Four different functions (blue lines) fit to the same set of training data (black dots). a), b), and c) reproduce the data, and d) does not.
The hypothesis space contains all hypotheses (i.e., functions) that could be returned by the learning algorithm. An appealing choice for a hypothesis space might be the space in which every possible function is considered to be equally viable. However there will be many functions in this space that exactly reproduce the training data (Figure 1), and there will be no way to determine which functions would make the most accurate predictions. Thus, to identify a predictive function, it is necessary to use a hypothesis space that is constrained in a way that excludes some functions from consideration and/or is weighted to favor some functions more than others. For example, it is common to constrain the hypothesis space so that only functions expressing a linear relationship between the input and output values are considered (Figure 1d).
There may be no function in the hypothesis space that produces the observed output values for all possible sets of input values. This could happen for some combination of several reasons:
- The hypothesis space has been constrained in a way that excludes the function that perfectly maps the input values to the output values. For example, the hypothesis space might be constrained to include only linear functions, whereas no linear function of the input variables can reproduce the observed output values (Figure 1d).
- The observed output values are the result of a process that is inherently non-deterministic.
- Some input data that are relevant to calculating the correct output values are missing and/or unknown.
In these situations, any function in the hypothesis space will result in some error in the predicted values. To account for this error, the output values can be expressed as:
| \[y = f\left( {\textbf{x}} \right) + E\] | [1] |
where $f$ is a function contained in the hypothesis space and $E$ is a random error. We will let $g$ represent the probability distribution from which $E$ is drawn. In other words, $g(a)$ is the probability density that $y - f({\bf{x}}) = a$. The distribution $g$ may depend on the input data, but for simplicity we will generally assume that it does not. In general, both the function $f$ and the probability distribution $g$ are unknown.
For a given probability distribution $g$, we can estimate the probability density that a function $f$ satisfies equation [1]. This probability density is expressed as $P\left( {f|{\bf{D}},g} \right)$, where ${\bf{D}}$ is the observed training data. This probability density can be evaluated using Bayes’ rule.1
Bayes’ rule is a fundamental statistical theorem that can be derived from the fact that the probability of two events, $A$ and $B$, occurring, is given by the probability of $B$ occurring times the conditional probability that $A$ occurs given that $B$ has occurred. Mathematically, this is written as:
| \[P\left( {A,B} \right) = P\left( B \right)P\left( {A|B} \right)\] | [2] |
Similarly,
| \[P\left( {A,B} \right) = P\left( A \right)P\left( {B|A} \right)\] | [3] |
Combining equations [2] and [3] yields Bayes’ rule:
| \[P\left( {A|B} \right) = \frac{{P\left( {B|A} \right)}}{{P\left( B \right)}}P\left( A \right)\] | [4] |
In the context of supervised learning, Bayes’ rule yields:
| \[P\left( {f|{\bf{D}},g} \right) = \frac{{P\left( {{\bf{D}}|f,g} \right)}}{{P\left( {{\bf{D}}|g} \right)}}P\left( {f|g} \right)\] | [5] |
The probability distribution $P\left( {f|g} \right)$ gives the probability density that a function $f$ satisfies equation [1] given $g$ and prior to the observation of any training data. For this reason, it is known as the prior probability distribution, which is sometimes simply referred to as the prior. The probability distribution $P\left( {f|{\bf{D}},g} \right)$ represents the probability of the same event after accounting for the training data. It is known as the posterior probability distribution. The distribution $P\left( {{\bf{D}}|f,g} \right)$, commonly known as the likelihood function, is the probability of observing the training data ${\bf{D}}$ given $f$ and $g$. The remaining term in equation [5], $P\left( {{\bf{D}}|g} \right)$, does not depend on $f$ and can effectively be treated as a normalization constant.
Bayes’ rule provides a natural and intuitive framework (or basis) for understanding learning. Initially, the hypothesis space is constrained and / or weighted through the prior probability distribution. All functions that are excluded from the hypothesis space are assigned a probability of zero, and functions that are not excluded are assigned non-zero prior probabilities. These probabilities represent the prior belief that any particular function satisfies equation [1]. As training data are observed, these probabilities are updated to account for the new knowledge, resulting in the posterior probability distribution – this is the learning step. If additional training data (${{\bf{D}}_{\bf{2}}}$) were to be observed, a re-application of Bayes’ rule could be used to update the probability distributions further:
| \[P\left( {f|{{\bf{D}}_2},{\bf{D}},g} \right) = \frac{{P\left( {{{\bf{D}}_2}|f,{\bf{D}},g} \right)}}{{P\left( {{{\bf{D}}_2}|{\bf{D}},g} \right)}}P\left( {f|{\bf{D}},g} \right)\] | [6] |
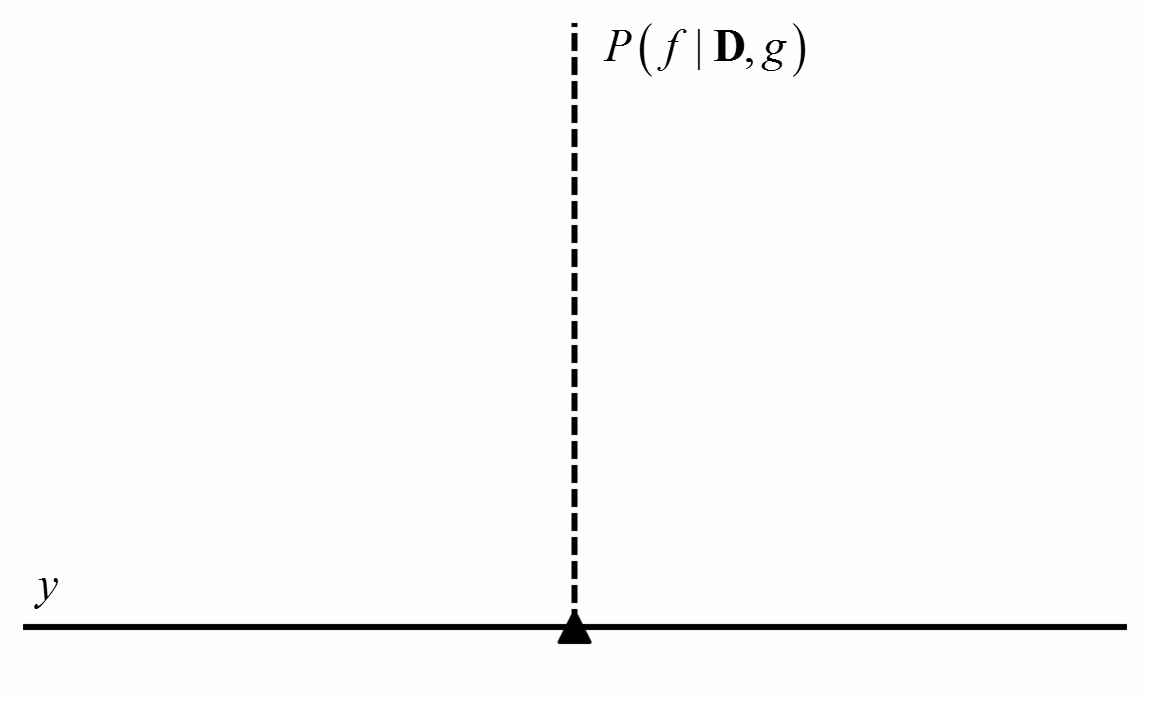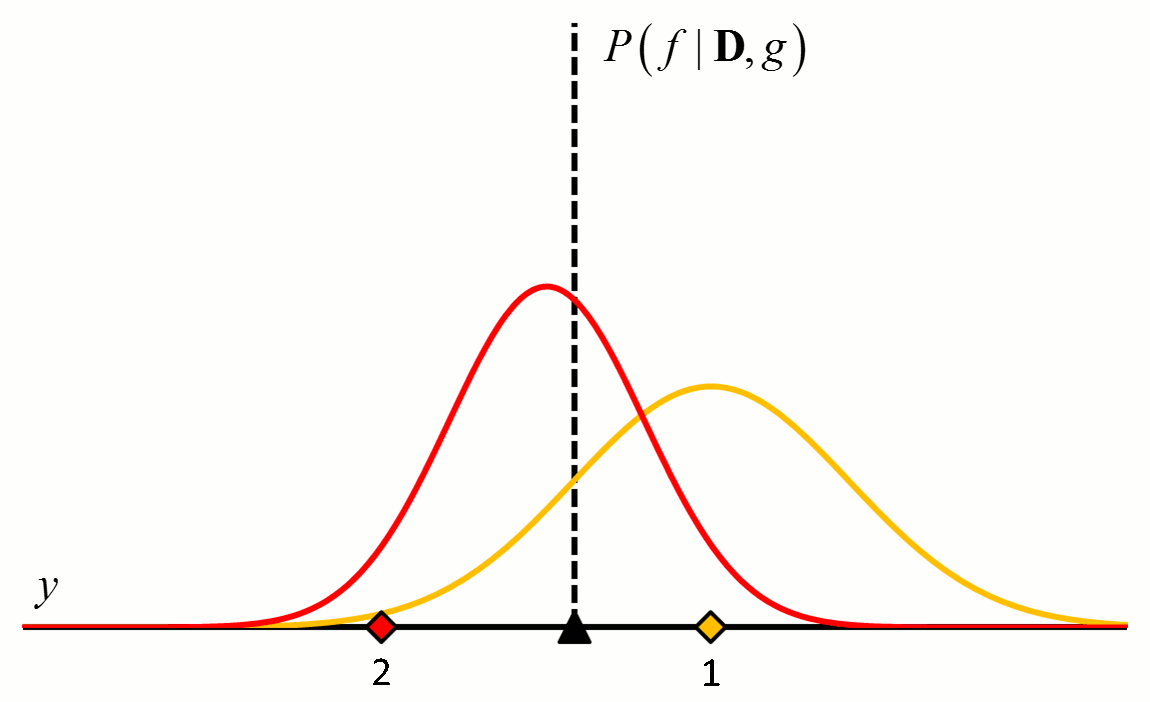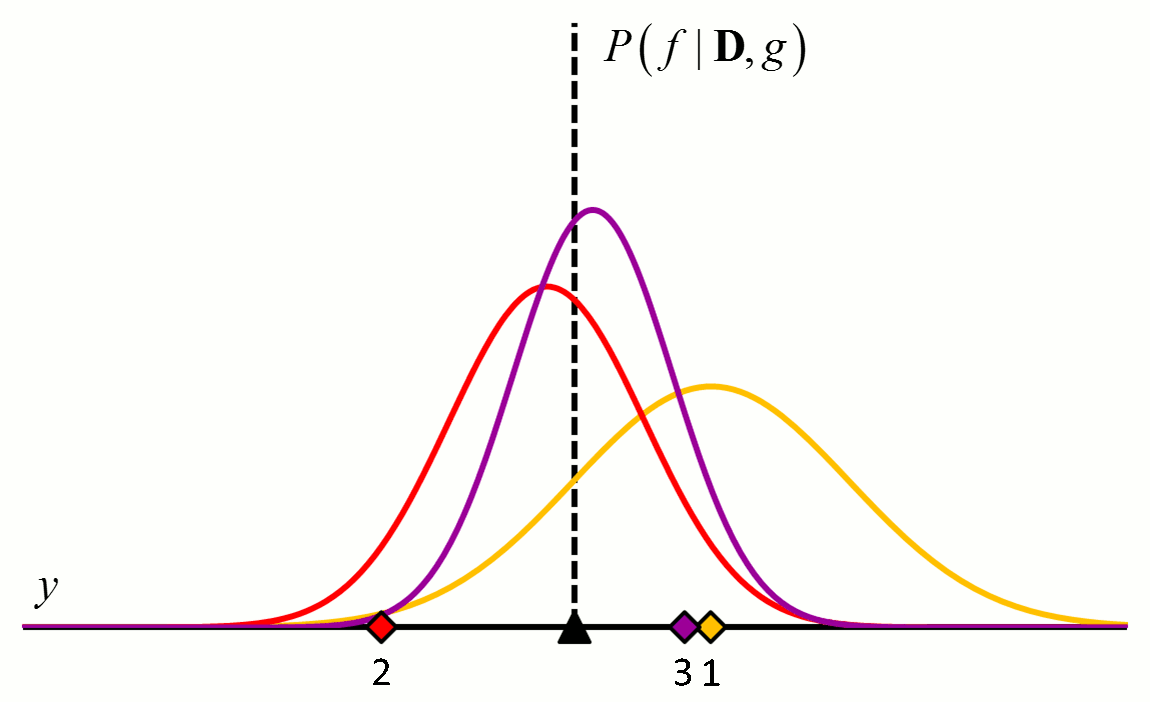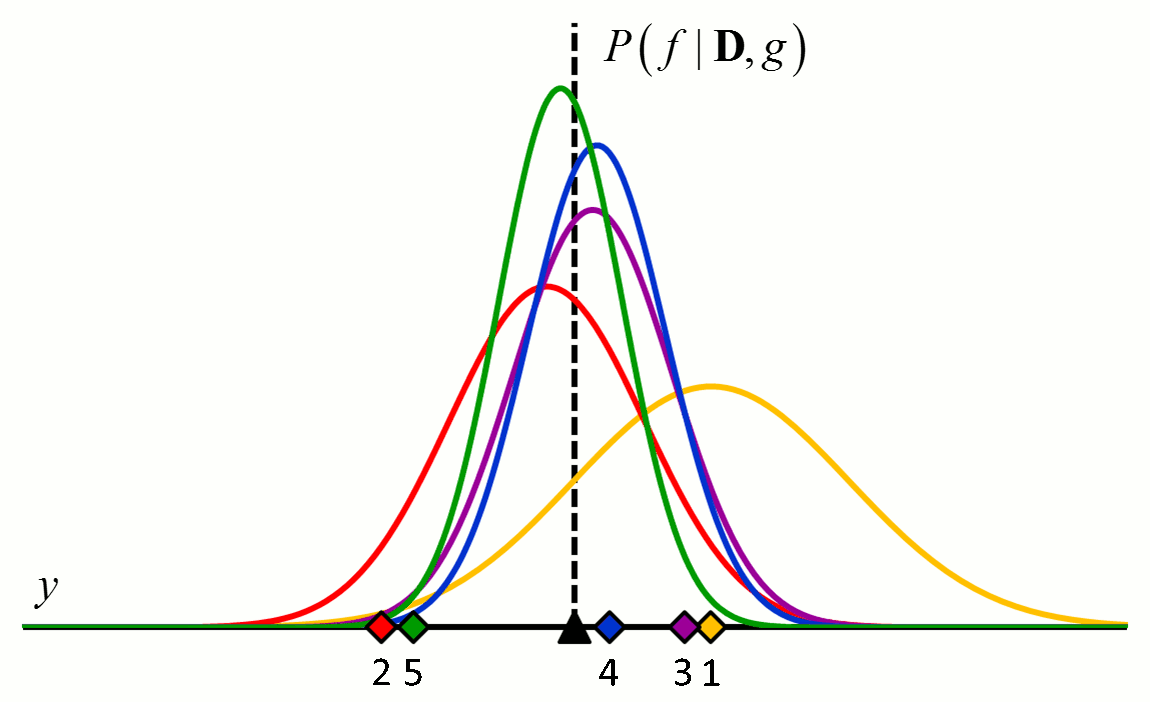
where the posterior distribution in equation [5] has become the prior distribution in equation [6]. Thus repeated application of Bayes’ rule can be used to update the likelihood that a particular hypothesis is best as new data come in. An example of how the posterior distributions change with new data points is shown in Figure 2.
Figure 2 An example of how the posterior probability density changes with the addition of new training data points. In this example, $f$ is a constant value indicated by the black triangle and $g$ is a normal distribution with zero mean and known variance. The diamonds represent training data. Assuming a uniform prior in which all values for $f$ are considered equally likely, the posterior probability densities for $f$ after the addition of the first (orange), second (red), third (purple), fourth (blue) and fifth (green) training data points are shown.
Because it can be awkward to deal with a probability distribution defined over many functions, learning algorithms will commonly return the single function $\hat f$ that maximizes the posterior probability density:
| \[\hat f = \mathop {\arg \max }\limits_f P\left( {f|{\bf{D}},g} \right)\] | [7] |
Combining equation [7] with equation [5] yields:
| \[\hat f = \mathop {\arg \max }\limits_f \left[ {P\left( {{\bf{D}}|f,g} \right)P\left( {f|g} \right)} \right]\] | [8] |
Because the natural log function is monotonically increasing, equation [8] can be equivalently written
| \[\hat f = \mathop {\arg \min }\limits_f \left[ { - \ln \left( {P\left( {{\bf{D}}|f,g} \right)} \right) - \ln \left( {P\left( {f|g} \right)} \right)} \right]\] | [9] |
The term in square brackets on the right side of equation [9] is the objective function to be minimized. The function with the maximum posterior probability of satisfying equation [1] is the function that minimizes the objective function. The idea of finding a function that minimizes an objective function is common to most machine learning algorithms, and the Bayesian analysis enables interpretation of the components of the objective function. The first term, $ - \ln \left( {P\left( {{\bf{D}}|f,g} \right)} \right)$, represents the empirical risk, a measure of how well a given function reproduces the training data. The second term, $ - \ln \left( {P\left( {f|g} \right)} \right)$, is the regularization term, representing the constraints and weights that are put on the hypothesis space before the training data are known.
Equation [9] is a commonly used framework for supervised learning algorithms. To determine the function $\hat f$ that is returned by the algorithm, there are five choices that typically need to be made. It is necessary to determine both what the hypothesis space should be and how the empirical risk will be calculated. There must also be an optimization algorithm that is capable of selecting a function from the hypothesis space (e.g., by minimizing the objective function). In addition, it is sometimes necessary to select the input values to be included in the training data and to estimate the prediction error for the selected function. In the following sections, each of these five choices is discussed in more detail.
It is through the prior probability distribution $P\left( {f|g} \right)$ that the hypothesis space is constrained and / or weighted. Thus selecting the prior probability distribution is equivalent to deciding which hypotheses will be considered and to what extent some hypotheses should be preferred over others. Hypotheses often take the form of models, or parameterized functions, for which the parameters are unknown. Often the prior distribution is implicitly specified simply by choice of the model to be used; for example, the assumption that a function is linear (as in Figure 1d) implicitly assigns zero prior probability to all non-linear functions.
The choice of the prior probability distribution can impact the effectiveness of the learning process significantly. Functions that are assigned a prior probability of zero are excluded from the hypothesis space and will not be considered no matter how strongly they are supported by the training data. On the other hand, a function that is assigned a small, but non-zero, prior probability could have a large posterior probability, provided it predicts the training data with relatively high accuracy. It is advantageous to choose prior distributions that assign the highest probability to the most accurate functions, as these distributions will generally result in an accurate choice of $\hat f$ with little (or no) additional training data.
The prior probability distribution is incorporated into the objective function through the regularization term, $ - \ln \left( {P\left( {f|g} \right)} \right)$. This term is often described as a way to penalize functions that are unlikely to make good predictions, and the benefit of a regularization term can be derived independently from Bayesian analysis.2 The use of a regularization term can make an ill-posed problem, in which there is no unique solution and/or the solution does not change continuously with the training data, into a problem that is well-posed.
The act of choosing a prior probability distribution can be controversial because it can introduce a subjective element into the learning process. However the choice of a prior must be made, either implicitly (e.g., by constraining the hypothesis space to only include certain functions) or explicitly. Five common strategies for selecting the prior probability distribution / regularization term are described below.
If no information is known about the process being modeled, a natural choice for the prior distribution would be one that makes the fewest assumptions about the relative merits of different candidate functions. Such prior probability distributions are known as uninformative priors. An uninformative prior distribution that assigns equal probabilities to all possible functions would make it impossible to differentiate between functions that perfectly reproduce the training data. Thus if an uninformative prior distribution is to be used among functions in the hypothesis space, it is necessary to constrain the hypothesis space to only include certain functions.
The appropriate choice of an uninformative prior may depend on the problem being modeled and the way in which the functions in the hypothesis space are parameterized. A number of different strategies have been proposed, and a thorough review of these can be found in reference 3. One strategy for choosing uninformative priors is the principle of maximum entropy, championed by E. T. Jaynes.4 This principle states that the prior probability distribution should be chosen in a way that maximizes the information entropy within the constraints of existing knowledge, where the information entropy of a probability density $p$ is a measure of uncertainty defined as
| $S\left( p \right) = - \int\limits_{ - \infty }^\infty {p\left( x \right)\ln \left( {p\left( x \right)} \right)dx} $ | [10] |
Jaynes has made the case that the distribution that maximizes the information entropy is the “maximally noncommittal” probability distribution.4 For example, if a single scalar parameter is to be determined, and nothing is known about it prior to the observation of the training data, then the principle of maximum entropy would state that the appropriate prior distribution is the uniform prior in which all possible values are considered equally likely.
A uniform prior that assigns equal prior probabilities to an infinite number of functions is an improper prior, in that it cannot be normalized to 1. In practice, such improper priors are widely used, as they may result in a proper (i.e., normalizable) posterior distribution.
One strategy for selecting a prior distribution is to evaluate multiple possible priors and choose the one giving the posterior distribution with the lowest expected prediction error. To this end, the methods described in the section “Estimating the Prediction Error” may be employed. A common variation of this approach is model selection, in which the learning process is broken into two steps. In the first step, a parameterized function (a.k.a model) is selected, effectively assigning zero prior probability to all other functions. (Different types of models are discussed in the section on “Supervised Learning Algorithms”; common examples include linear models, neural networks, etc.) In the second step the parameter values that minimize the objective function for the selected model are determined.
A general approach to model selection can be derived through a Bayesian analysis. For a given model and a given set of training data, different values of the model parameters will result in different values for the empirical risk. Let $r$ represent the minimum value of the empirical risk achievable within a given model for a given set of training data. Schwartz demonstrated that under a wide range of conditions, the model with the greatest expected posterior probability is the one for which the following value is smallest:
| \[2r + k\ln \left( n \right)\] | [11] |
where $k$ is the number of parameters in the model and $n$ is the number of elements (${\bf{x}},y$ pairs) in the training data.5 The expression in equation [11] is commonly known as the Bayesian information criterion (BIC). Separately, Akaike derived a similar term to be minimized for model selection, commonly known as the Akaike information criterion (AIC):6
| \[2r + 2k\] | [12] |
Both the Bayesian information criterion and Akaike information criterion are valuable for revealing a general rule for model selection: among models that reproduce the training data equally well, the one with the fewest parameters can be expected to have the lowest prediction error. This result is similar to Occam’s razor, a commonly used heuristic that all else being equal, simple hypotheses should be favored over more complex ones. Intuitively, this insight can be understood by considering that if there are more parameters in a model, there is greater risk of selecting a function that happens to reproduce the training data well but has little predictive ability. This is known as overfitting the training data.
Determining the best way to constrain and/or weight the hypothesis space can be accomplished by incorporating prior knowledge about the process being modeled into the prior distribution. For example, physical arguments might suggest that the output value should be a linear function of a particular input value, or the expected magnitudes of some of the parameters that define the function might be known. The prior probability distribution can be constructed in a way that accounts for this knowledge, directing the learning process towards functions that are expected to be reasonable even before the observation of the training data. The use of a prior probability distribution that effectively takes into account external knowledge can significantly accelerate the learning process by making use of all available knowledge.
The principle of maximum entropy can be combined with prior knowledge to create a prior distribution that incorporates existing knowledge in a “maximally noncommittal” way. For example, if estimates for the mean and the variance of a parameter’s value are available, then a Gaussian distribution over possible parameter values will maximize the information entropy and would therefore be the appropriate choice of a prior distribution for the parameter value under the principle of maximum entropy.
Prior knowledge can be especially useful for setting the mean of the prior probability distribution. If the prior probability distribution has a non-zero mean $\bar f$, then the learning process can be re-cast in terms of a prior probability distribution with zero mean by replacing the function $f$ with
| $\Delta f = f - \bar f$ | [13] |
Accordingly, each value ${y_i}$ in the training data is replaced with
| \[\Delta {y_i} = {y_i} - \bar f\left( {{{\bf{x}}_i}} \right)\] | [14] |
For example, if $f$ calculates the energy of a compound, then $\bar f$ might be the composition-weighted average of the energies of the constitutive elements, and $\Delta f$ would be the formation energy.
The function $\Delta f$ represents the difference between the actual function $f$ and the expected function $\bar f$. Because $f$ is expected to resemble $\bar f$, it can be expected that the norm of $\Delta f$, represented by $\left\| {\Delta f} \right\|$, is more likely to be small than it is to be large. For this reason, it is common to use a term that monotonically increases with $\left\| {\Delta f} \right\|$ as the regularization term.
A variety of different norms can be used, and some of the most popular take the form of the ${L^p}$ norm, defined by
| $\left\| f \right\| = {\left( {\int {{{\left| {f\left( {\bf{x}} \right)} \right|}^p}d{\bf{x}}} } \right)^{1/p}}$ | [15] |
where p ≥ 1 and the integral is over all values of x. The ${L^1}$ and ${L^2}$ norms are commonly used, as are smoothing norms that favor functions that vary smoothly with the input values (i.e., their higher-order derivatives are small). An example of a widely used smoothing norm is the ${L^2}$ norm of the second derivative of $\Delta f$.
It is generally a good idea to transform $f$ to $\Delta f$ if prior knowledge can be used to make a reasonable estimate for $\bar f$; otherwise $\bar f = 0$ is implicitly used. The approaches to supervised learning discussed in this chapter are equally applicable to $f$ and $\Delta f$.
An alternative approach to selecting a particular prior distribution is to assign a probability distribution over the space of possible prior distributions. Such a probability distribution is known as a hyperprior. For example, if a Gaussian distribution with zero mean is used as the prior, a hyperprior could be constructed as a probability distribution over possible values of the variance of the Gaussian. The posterior distribution can then be calculated as a weighted average over prior distributions:
| \[P\left( {f|{\bf{D}},g} \right) = \int {\frac{{P\left( {{\bf{D}}|f,g} \right)}}{{P\left( {{\bf{D}}|g} \right)}}P\left( {f|g} \right)} P\left( {P\left( {f|g} \right)} \right)\] | [16] |
where $P\left( {f|g} \right)$ is the prior, $P\left( {P\left( {f|g} \right)} \right)$ is the hyperprior, and the integral is over all possible prior distributions.
Many of the same challenges for determining a prior exist for determining a hyperprior, and there is an extra integration step that needs to be performed to arrive at the posterior. However the hyperprior allows for an extra layer of abstraction in situations in which the posterior may be particularly sensitive to the choice of a prior. It is possible to similarly define hyperhyperpriors, etc, but in practice this is rarely done.
The empirical risk represents the negative log probability of observing the training data for a given $f$ and $g$. Assuming that all of the observations in the training data are independent, from equation [1] and the definition of $g$, we can write:
| \[P\left( {{\bf{D}}|f,g} \right) = \prod\limits_i {g\left( {{y_i} - f\left( {{{\bf{x}}_i}} \right)} \right)} \] | [17] |
where ${{\bf{x}}_i}$ is the ${i^{th}}$ set of input values in the training set, ${y_i}$ is the ${i^{th}}$ output value, and the product is over all elements in the training set. Thus, under the assumption that the observations in the training set are independent of each other, the empirical risk can be written as:
| \[ - \ln \left( {P\left( {{\bf{D}}|f,g} \right)} \right) = \sum\limits_i { - \ln \left( {g\left( {{y_i} - f\left( {{{\bf{x}}_i}} \right)} \right)} \right)} \] | [18] |
where the sum is over all elements in the training set. For example, if $g$ is assumed to be Gaussian, then the empirical risk would depend on the sum of the squared differences between ${y_i}$ and $f\left( {{{\bf{x}}_i}} \right)$. This approach leads to least-squares fitting, discussed in more detail in the section on “Regularized Least Squares”.
The empirical risk is sometimes written more generally as
| \[\sum\limits_i {L\left( {{y_i},f\left( {{{\bf{x}}_i}} \right)} \right)} \] | [19] |
where $L$ is a loss function that calculates the penalty (a.k.a loss) for large differences between ${y_i}$ and$f\left( {{{\bf{x}}_i}} \right)$. In practice many commonly used loss functions can be written in the form of equation [18], as a function of ${y_i} - f\left( {{{\bf{x}}_i}} \right)$.
Unlike the prior probability distribution, the empirical risk depends on the function$g$, which is in general unknown. As both $f$ and $g$ are unknown, it might make sense to treat the two similarly and to search for the pair of functions that together are most likely to satisfy equation [1]. The posterior and prior distributions would then be defined for the pair, $(f,g)$, and application of Bayes’ rule would yield:
| \[P\left( {f,g|{\bf{D}}} \right) = \frac{{P\left( {{\bf{D}}|f,g} \right)}}{{P\left( {\bf{D}} \right)}}P\left( {f,g} \right)\] | [20] |
as an alternative to equation [5]. However such an approach is not commonly used. Instead, it is more common to make the prior assumption that $g$, and hence the loss function, is known.
If a uniform prior probability distribution is used for all functions in the hypothesis spaces, then the optimization of the objective function (equation [9]) can be accomplished by minimizing the empirical risk. This approach is known empirical risk minimization. Empirical risk minimization is equivalent to selecting the function that maximizes the likelihood function \[P\left( {{\bf{D}}|f,g} \right)\] (i.e., the function that best reproduces the training data). Although empirical risk minimization is a widely used method, there is a risk of overfitting training data. This risk can often be mitigated by replacing the uniform prior used in empirical risk minimization with a prior distribution that favors simple functions or takes into account prior knowledge.
Many machine learning algorithms involve the optimization of an objective function, as in equation [9]. For practical purposes, the functions in the hypothesis space are typically characterized by a set of unknown parameters; e.g., the functions may be expressed as a linear combination of basis functions, in which the linear expansion coefficients are unknown parameters. Thus the problem of searching for the optimal function becomes a problem of finding the set of parameters that minimize the objective function. Many algorithms have been developed to address such optimization problems (e.g., gradient descent approaches, simulated annealing, etc.), and the field of general optimization algorithms is too large to discuss here. Instead we refer the reader to some of the many comprehensive books on the subject (e.g., references 7-9).
For some objective functions, there may be no known algorithm that is able to find the globally optimal function and / or verify whether a particular function is globally optimal with a reasonable computational cost. However many machine learning algorithms use an objective function and hypothesis space that have been designed to facilitate the rapid identification of the globally optimal function. The ways in which this is done are described in the context of individual machine learning algorithms in the section on “Supervised Learning Algorithms”.
The training data may be generated by observations of external events that cannot easily be controlled, such as climatological data used in weather forecasting. However in many cases it is possible to generate training data through controlled experiments. In each experiment, a set of input values are evaluated, and the corresponding output value becomes known once the experiment is complete. Because the generation of training data can be an expensive and/or time-consuming step in the learning process, it is desirable to minimize the total number of experiments that must be performed to achieve an acceptable level of prediction error. The field of active learning, also known as design of experiments, deals with determining the best set of experiments to perform (i.e. determining the best elements to include in training data) to minimize the total cost of generating the training data.
There are many different approaches to active learning, and we will not review them all here. Good overviews can be found in references 10-12. A common approach to active learning is uncertainty sampling,13 in which the next experiment is performed on input values for which there is a large amount of uncertainty in the predicted output value. A related approach is query by committee,14 in which several different models are trained on the same data, and the next experiment is performed on a data point about which there is the least agreement among the models. However this approach can result in the sampling of outlier data points that are not representative of the space of possible input values. Alternatively, if the distribution of all possible input values is known, the input values can be selected in a way that takes this distribution into account. Such density-weighted methods can result in significant performance improvements over methods that do not account for the distribution of possible input values.11
If the hypothesis space consists of parameterized functions, the training data may be chosen in a way that minimizes some measure of the variance of the estimated parameter values. This is often accomplished by optimizing the observed information matrix, sometimes called simply the information matrix.15 The observed information matrix is the Hessian of the empirical risk with respect to the function parameters, and it is often evaluated at the parameter values that minimize the empirical risk. It is an indicator of how informative the current training data are about the parameter values.
A number of different criteria have been developed to optimize the observed information matrix. Among the most common are A-optimality, in which the trace of the inverse information matrix is minimized, and D-optimality, in which the determinant of the information matrix is maximized.16-18 An overview of these and many other optimality criteria can be found in reference 19. As the information matrix does not take into account the prior probability distribution over possible parameter values, an alternative approach is to use the Hessian of the objective function in place of the information matrix. In this approach, sometimes referred to as Bayesian experimental design,20, 21 the same matrix optimality criteria (A-optimality, D-optimality, etc.) may be used. In materials science, optimization of the information matrix has been used to select training data for cluster expansion models.
The goal of a machine learning algorithm is to identify a function that makes accurate predictions for input values that are not included in the training data. Thus to evaluate the results of a learning algorithm, it is not sufficient to evaluate how well the function reproduces the training data (i.e., the empirical risk). Rather it is best to use a method that is capable of estimating the prediction error of a function over the distribution of all possible input values.
The estimation of the prediction error can be accomplished using resampling methods, in which functions are trained on one or more subsamples of the training data using the same learning algorithm that is used for the entire set of training data. These functions are then evaluated using subsamples of the training data on which they were not trained, providing an estimate of the predictive ability of the functions identified by the learning algorithm.
A common resampling technique is cross-validation,22-25 in which the set of known observations are partitioned into two subsets. The first subset, the training set, is used to identify a likely function. The predictive power of this function is evaluated by calculating its prediction error when applied to the second subset, known as the test set. Averaging the cross-validation prediction error over multiple different partitions provides a measure of the estimated prediction error for a function trained on the entire known set of observations. A common variation of cross-validation approach is k-fold cross validation, in which the set of observations are partitioned into k different subsets, and the prediction error on each subset is evaluated for a function trained on the k-1 remaining subsets. When k equals the number of samples in the training set, this approach is known as leave-one-out cross validation.
Another popular resampling technique is bootstrapping,26-28 in which the subsamples are drawn from the set of training data with replacement, meaning the same element can appear in the subsample more than once. Functions trained on these subsamples are then compared to a function trained on the entire set of training data. Bootstrapping is commonly used to estimate statistics such as the bias and variance in the output of the learning algorithm. Additional details about cross-validation, bootstrapping, and other resampling methods can be found in references 29-33.
Resampling methods provide the best estimates of prediction error when the distribution of input values in the set of known observations is representative of the distribution of all possible input values. Training data that consist of uncontrollable empirical observations generally fit this description, provided the observations are effectively randomly drawn from the distribution of all possible input values. Alternatively, density-weighted active learning methods can generate a set of observations that are representative of the distribution of possible input values and are well-suited for use in cross-validation algorithms.
Many supervised learning algorithms have been developed, and it is not feasible to describe them all here. Instead, a brief overview of some of the most common approaches is provided. These approaches are all described in the context of the framework presented in the Introduction. In each of these approaches, there is a hypothesis space, objective function, and optimization algorithm. There are also sometimes algorithm-specific active learning methods used to generate an efficient set of training data. Approaches for estimating prediction error are fairly universal, so they will not be described in detail here.
One of the most widely used methods for fitting a function to data is least squares regression. The least-squares approach is characterized by the assumption that $g$ is Gaussian:
| \[g\left( {{y_i} - f\left( {{{\bf{x}}_i}} \right)} \right) = \frac{1}{{\sigma \sqrt {2\pi } }}{e^{\frac{{{{\left( {{y_i} - f\left( {{{\bf{x}}_i}} \right)} \right)}^2}}}{{2{\sigma ^2}}}}}\] | [21] |
The empirical risk is therefore:
| \[ - \ln \left( {P\left( {{\bf{D}}|f,g} \right)} \right) = \frac{1}{{2{\sigma ^2}}}\sum\limits_i {\left[ {{{\left( {{y_i} - f\left( {{{\bf{x}}_i}} \right)} \right)}^2} - \ln \left( {\frac{1}{{\sigma \sqrt {2\pi } }}} \right)} \right]} \] | [22] |
where the sum is over all elements in the training set. The loss function depends on the squared difference between the observed and predicted output values, and empirical risk minimization yields:
| \[\hat f = \mathop {\arg \min }\limits_f \sum\limits_i {{{\left( {{y_i} - f\left( {{{\bf{x}}_i}} \right)} \right)}^2}} \] | [23] |
Equation [23] describes a least-squares fit, in which the selected function minimizes the sum of the squared errors over all of the elements in the training set. The loss function in equation [23], known as the squared error loss, is commonly used in machine learning algorithms. Under the assumptions that the errors are normally distributed with zero mean and constant variance (equation [21]), the least squares fit returns the function that maximizes the probability of observing the training data. Similarly, if a uniform prior is assumed for the functions in the hypothesis space, the least-squares fit returns the function that maximizes the posterior probability distribution.
The least-squares fit is often a justifiable choice for function fitting. The assumption that $g$ is Gaussian can be justified using the principle of maximum entropy, and the use of a uniform prior can be justified on the grounds that it is uninformative and hence will not bias the results. Perhaps most importantly from a practical perspective, the least-squares fit is conceptually simple and easy to implement. In a common implementation, known as linear least squares or ordinary least squares, the hypothesis space is restricted to include only linear functions of the input values. The optimal set of coefficients, ${\bf{\hat \beta }}$, is given by
| \[{\bf{\hat \beta }} = \mathop {\arg \min }\limits_\beta \sum\limits_i {{{\left( {{y_i} - {{\bf{x}}_i}{\bf{\beta }}} \right)}^2}} \] | [24] |
where ${{\bf{x}}_i}$ is a row-vector containing the input values and ${\bf{\beta }}$ is a column-vector containing the unknown input values. From equation [24], the exact optimal solution can be calculated:
| \[{\bf{\hat \beta }} = {\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}}} \right)^{ - 1}}{{\bf{X}}^{\bf{T}}}{\bf{y}}\] | [25] |
where ${\bf{y}}$ is a column-vector in which the ith element is ${y_i}$, and ${\bf{X}}$ is a matrix in which the ith row is ${{\bf{x}}_i}$. A unique solution to equation [25] only exists if the matrix ${{\bf{X}}^{\bf{T}}}{\bf{X}}$ is non-singular.
It is often possible to improve upon least squares fits by using a non-uniform prior distribution. For example, consider the situation in which a multivariate normal distribution is used as the prior:
| \[P\left( {{\bf{\beta }}|g} \right) \propto {e^{\frac{{ - {{\bf{\beta }}^T}{\bf{\Lambda \beta }}}}{{2{\sigma ^2}}}}}\] | [26] |
where ${\bf{\Lambda }}$ is a positive-definite matrix. The set of coefficients that minimize the objective function is given by
| \[{\bf{\hat \beta }} = {\left( {{{\bf{X}}^{\bf{T}}}{\bf{X}} + {\bf{\Lambda }}} \right)^{ - 1}}{{\bf{X}}^{\bf{T}}}{\bf{y}}\] | [27] |
Equation [27] represents a type of regularized least-squares fit known as Tikhonov regularization.2 When a normal least-squares fit is ill-posed (e.g., when ${{\bf{X}}^{\bf{T}}}{\bf{X}}$ is singular), Tikhonov regularization can make the problem well-posed, such that a unique solution is guaranteed. Variants of Tikhonov regularization are popular in part because they are often easy to justify, robust, and the optimal solution can be found with only slightly more computational cost than a least-squares fit.
When ${\bf{\Lambda }} = \lambda {\bf{I}}$ in equation [27], where ${\bf{I}}$ is the identity matrix, it is known as ridge regression.34 Ridge regression is equivalent to using the squared ${\ell ^2}$ norm of the coefficients as the regularization term, where the ${\ell ^p}$ norm for a vector is defined as
| \[\left\| {\bf{\beta }} \right\| = {\left( {\sum\limits_i {{\beta _i}^p} } \right)^{1/p}}\] | [28] |
for p ≥ 1. (It is the discrete version of the ${L^p}$ norm described by equation [15].) Another popular form of regularized least-squares includes the use of an ${\ell ^1}$ norm instead of an ${\ell ^2}$ norm. The use of the ${\ell ^1}$ norm often results in a minimizing vector of coefficients, ${\bf{\hat \beta }}$, in which many elements are identically 0. This approach is sometimes known as the Lasso estimator or compressive sensing,35, 36 and it is useful when the solution is sparse. It is in general not as straightforward as using the ${\ell ^2}$ norm, but efficient algorithms for finding the optimal set of coefficients exist.37
Linear least squares is a particularly convenient method for active learning approaches (described in the section on "Training Data"), as the information matrix is independent of the values of the coefficients and proportional to ${{\bf{X}}^{\bf{T}}}{\bf{X}}$. For Bayesian experimental design, the matrix ${{\bf{X}}^{\bf{T}}}{\bf{X}} + {\bf{\Lambda }}$ may be used in place of ${{\bf{X}}^{\bf{T}}}{\bf{X}}$.
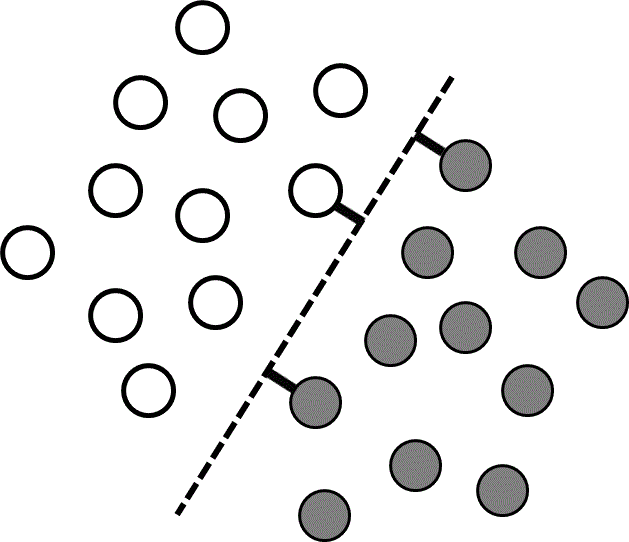
Classification problems differ from regression problems in that the set of allowed output values is discrete, with each allowed output value corresponding to a different class. The same general learning framework could be used for classification problems as for regression problems, but in practice it can be difficult to work with discontinuous output values. Many classification problems can be simplified by recognizing that different classes often correspond to different regions in input-value space (Figure 3). Thus instead of searching for a discontinuous function that predicts the output values directly, it is possible to search instead for a continuous dividing surface between the regions corresponding to different classes.
For example, consider a situation in which there are two classes, corresponding to $y = 1$ and $y = - 1$. If the prior assumption is made that there is a linear hyperplane in the space of input values that divides the two different classes, then the classification function takes the form:
| \[f\left( {\bf{x}} \right) = \left\{ {\begin{array}{*{20}{c}} {1,} & {{\rm{if\hspace{1em}}}{\bf{w}} \cdot {\bf{x}} - b > 0}\\ { - 1,} & {{\rm{if\hspace{1em}}}{\bf{w}} \cdot {\bf{x}} - b < 0} \end{array}} \right.\] | [29] |
where the vector of coefficients ${\bf{w}}$ (commonly known as weights) and the offset $b$ define the hyperplane that divides the two classes (Figure 3). Thus the discrete classification function, $f\left( {\bf{x}} \right)$, can be determined by learning the continuous function ${\bf{w}} \cdot {\bf{x}} - b$. We will call this continuous function $h\left( {\bf{x}} \right)$.
The training data are linearly separable if there is at least one hyperplane that perfectly separates the two classes. There are usually many competing hyperplanes that can separate linearly separable data, and the goal of the learning algorithm is to find the one that is most likely to correctly separate data points that are not in the training set. One approach is to find the hyperplane that is farthest from the input values in the training data. In other words, the best hyperplane is the one with the longest support vectors, which are defined as the shortest vectors between the hyperplane and the nearest training data point of each class (Figure 3). Support vector machines are widely used supervised learning algorithms that identify such a hyperplane.38 If there are more than two different classes present, support vector machines can be used to find the hyperplanes separating all pairs of classes. A brief introduction to support vector machines is presented below, and a more comprehensive review of different support vector machine approaches can be found in references 39 and 40.
Figure 3 A linearly separable data set containing two classes (grey and white). Each point corresponds to coordinates $\left( {{x_1},{x_2}} \right)$ given by the input values, and the colors are determined by the corresponding $y$ values. The dashed line shows the dividing plane, and the short thick lines are the support vectors.
Hyperplanes are defined by the unknown parameters ${\bf{w}}$ and $b$, and the optimal values for these parameters can be found by minimizing an objective function similar to the one in equation [9]. The loss function ( equation [19]) is given by
| \[L\left( {{y_i},h\left( {{{\bf{x}}_i}} \right)} \right) = \left\{ {\begin{array}{*{20}{c}} {0,} & {{\rm{if\hspace{1em} }}{y_i}h\left( {{{\bf{x}}_i}} \right) \ge 1}\\ {\infty ,} & {{\rm{if\hspace{1em}}}{y_i}h\left( {{{\bf{x}}_i}} \right) < 1} \end{array}} \right.\] | [30] |
and the regularization term is simply $\frac{1}{2}{\left\| {\bf{w}} \right\|^2}$. The loss function ensures that the plane separates the two classes, and the regularization term is minimized for the plane with the longest support vectors. This is a constrained quadratic optimization problem that can be solved using quadratic programming.41, 42 A similar approach, least-squares support vector machines (LS-SVM),43 enables the calculation of the optimal weights by solving a linear system.
If the training data are not linearly separable, then the loss function in equation [30] will always be infinite for at least one element of the training set, and no optimal set of parameters will be found. This problem can be addressed by introducing non-negative slack variables, ${\xi _i}$, that allow for some data points to be misclassified.38 The slack variables effectively measure the distance between the hyperplane and the misclassified data points. The loss function becomes:
| \[L\left( {{y_i},h\left( {{{\bf{x}}_i}} \right)} \right) = \left\{ {\begin{array}{*{20}{c}} {0,} & {{\rm{if\hspace{1em}}}{y_i}h\left( {{{\bf{x}}_i}} \right) \ge 1 - {\xi _i}}\\ {\infty ,} & {{\rm{if\hspace{1em}}}{y_i}h\left( {{{\bf{x}}_i}} \right) < 1 - {\xi _i}} \end{array}} \right.\] | [31] |
and the regularization term is $\frac{1}{2}{\left\| {\bf{w}} \right\|^2} + C\sum\limits_i {{\xi _i}} $, where $C$ is an adjustable parameter that determines how severely misclassification should be penalized. An alternative equivalent formulation is to use the hinge loss:
| \[L\left( {{y_i},h\left( {{{\bf{x}}_i}} \right)} \right) = \left\{ {\begin{array}{*{20}{c}} {0,} & {{\rm{if\hspace{1em} }}{y_i}h\left( {{{\bf{x}}_i}} \right) \ge 1}\\ {C\left( {1 - {y_i}h\left( {{{\bf{x}}_i}} \right)} \right),} & {{\rm{if\hspace{1em}}}{y_i}h\left( {{{\bf{x}}_i}} \right) < 1} \end{array}} \right.\] | [32] |
where the corresponding regularization term is $\frac{1}{2}{\left\| {\bf{w}} \right\|^2}$. By comparing the loss functions in equations [30] and [32], it can be seen that the hinge loss simply replaces the infinite penalty for misclassification with a penalty that scales linearly with the degree of misclassification.
The optimal set of weights for support vector machines can be found be solving the dual problem, in which the weights are written as
| \[{\bf{w}} = \sum\limits_i {{\alpha _i}} {y_i}{{\bf{x}}_i}\] | [33] |
where the sum is over all elements in the training set. The vector of coefficients ${\bf{\alpha }}$ is given by
| \[\mathop {\arg \max }\limits_{\bf{\alpha }} \left( {\sum\limits_i {{\alpha _i}} - \sum\limits_i {\sum\limits_j {{\alpha _i}{\alpha _j}{y_i}{y_j}\left( {{{\bf{x}}_i} \cdot {{\bf{x}}_j}} \right)} } } \right)\] | [34] |
subject to the constraints
| \[\begin{array}{l} 0 \le {\alpha _i} \le C,\\ \sum\limits_i {{\alpha _i}{y_i}} = 0 \end{array}\] | [35] |
where each sum is over all elements in the training set. The dual problem formulation makes it possible to use support vector machines to classify data that are not linearly separable using the kernel trick, in which the input variables are transformed in a way that makes the data linearly separable.
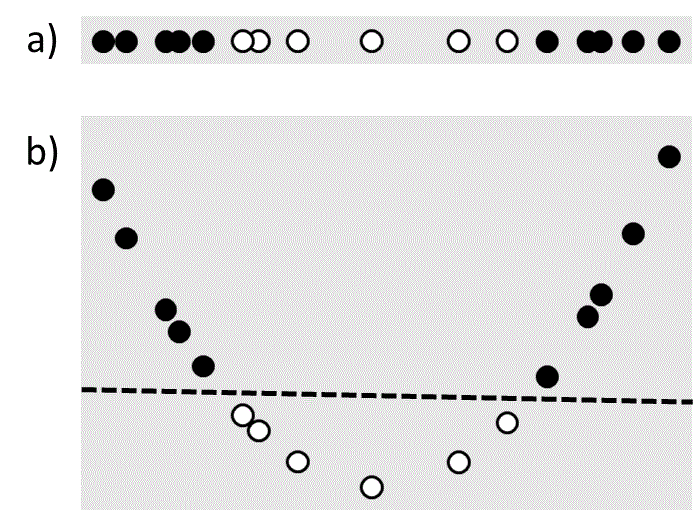
Linear least squares and support vector machines are popular due to their speed and simplicity, which come from the underlying assumption that the solution must be a linear function of the input variables. However in many cases this assumption is unrealistic. For example, consider the classification problem shown in Figure 4a. There is no linear plane that will separate the data, which means that a linear support vector machine will fail to find a good solution. However it is possible to transform the original one-dimensional input value $\left( {{x_1}} \right)$ to a two-dimensional feature space, $\left( {{x_1},{x_1}^2} \right)$, in which linear separation is possible (Figure 4b). Such transformations of the input variables are known as feature maps.
Figure 4 a) A one-dimensional data set that is not linearly separable. b) The same data set mapped to two dimensions using a feature map that makes it linearly separable. The dashed line is the separating plane.
Feature maps can be used in machine learning algorithms by simply substituting the transformed input variables, $\varphi \left( {\bf{x}} \right)$, for the original input variables ${\bf{x}}$. However in some cases, such as when the feature space has an infinite number of dimensions, it may not be practical to explicitly make such a transformation. Alternatively, many algorithms, including support vector machines (equation [34]) and linear least squares, can be expressed in a way that depends only on the input variables through inner products such as ${{\bf{x}}_1} \cdot {{\bf{x}}_2}$. In such cases, it is sufficient to find a kernel $k\left( {{{\bf{x}}_i},{{\bf{x}}_j}} \right)$ that returns the dot product between $\varphi \left( {{{\bf{x}}_i}} \right)$ and $\varphi \left( {{{\bf{x}}_j}} \right)$:
| $k\left( {{{\bf{x}}_i},{{\bf{x}}_j}} \right) \equiv \varphi \left( {{{\bf{x}}_i}} \right) \cdot \varphi \left( {{{\bf{x}}_j}} \right)$ | [36] |
To use a learning algorithm in a given feature space, all that needs to be done is to use the kernel $k\left( {{{\bf{x}}_i},{{\bf{x}}_j}} \right)$ in place of the inner product ${{\bf{x}}_i} \cdot {{\bf{x}}_j}$ throughout the learning algorithm. This is known as the kernel trick.44
The direct use of the kernel function saves the trouble of having to apply a feature map and calculate the inner products explicitly. When using the kernel trick, it is not even necessary to know which feature maps produce the kernel -- any symmetric, continuous, positive definite kernel can be used, as every such kernel corresponds to an inner product in some feature space.45 (A positive definite kernel is defined as a kernel for which $\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{c_i}{c_j}k({{\bf{x}}_{\bf{i}}},{{\bf{x}}_{\bf{j}}})} } \ge 0$ for any real-valued $\left\{ {{c_1},\;...\;,{c_n}} \right\}$and $\left\{ {{{\bf{x}}_1},\;...\;,{{\bf{x}}_n}} \right\}$.) Such kernels are known as Mercer kernels or reproducing kernels. Some examples of reproducing kernels are shown in Table I.
|
Name |
$k({{\bf{x}}_i},{{\bf{x}}_j})$ |
|
Linear |
${{\bf{x}}_i} \cdot {{\bf{x}}_j} + c$ |
|
Polynomial kernel |
${\left( {{c_1}\left( {{{\bf{x}}_i} \cdot {{\bf{x}}_j}} \right) + {c_2}} \right)^d}$ |
|
Gaussian |
${e^{\frac{{ - {{\left\| {{{\bf{x}}_i} - {{\bf{x}}_j}} \right\|}^2}}}{{2{\sigma ^2}}}}}$ |
|
Laplacian |
${e^{\frac{{ - \left\| {{{\bf{x}}_i} - {{\bf{x}}_j}} \right\|}}{\sigma }}}$ |
Table I Examples of symmetric, continuous, positive definite kernels. The scalar parameters $c$, ${c_1}$, ${c_2}$, and $\sigma $ are all adjustable, with the constraints that $\sigma $ and ${c_1}$ are positive and $d$ is a positive integer.
For a reproducing kernel$k\left( {{{\bf{x}}_1},{{\bf{x}}_2}} \right)$, consider the space of functions $f$ that are given by
| $f\left( {\bf{x}} \right) \equiv \sum\limits_j {{\alpha _j}k\left( {{{\bf{x}}_j},{\bf{x}}} \right)} $ | [37] |
where ${\alpha _j}$ are scalar coefficients and the sum may contain any number of terms. The inner product ${\left\langle {} \right\rangle _H}$ on this space is defined such that:
| ${\left\langle {k\left( {{{\bf{x}}_i},{\bf{x}}} \right),k\left( {{{\bf{x}}_j},{\bf{x}}} \right)} \right\rangle _H} = k\left( {{{\bf{x}}_i},{{\bf{x}}_j}} \right)$ | [38] |
This function space is known as a reproducing kernel Hilbert space (RKHS) 46. Each RKHS has a norm, ${\left\| f \right\|_H}$, which is defined as
| \[{\left\| f \right\|_H} \equiv \sqrt {{{\left\langle {f,f} \right\rangle }_H}} \] | [39] |
The norm of the RKHS depends on the underlying kernel. For example, the norm of the linear RKHS is given by
| \[\left\| f \right\|_{_H}^2 = {w^2}\] | [40] |
where $f\left( x \right) = wx$. Thus in a linear RKHS, functions with a steeper slope will have larger norms. The norm of the Gaussian RKHS is
| \[\left\| f \right\|_{_H}^2 = \int\limits_{ - \infty }^\infty {F{{\left( \omega \right)}^2}{e^{\frac{{{\sigma ^2}{\omega ^2}}}{2}}}d\omega } \] | [41] |
where $F\left( \omega \right)$ is the Fourier transform of$f\left( x \right)$. Thus in the Gaussian RKHS, functions that fluctuate more rapidly will have larger norms.
Reproducing kernel Hilbert spaces have special properties that make them particularly useful for supervised machine learning. Consider a situation in which the hypothesis space is a RKHS. If a Gaussian kernel is used, for example, the hypothesis space would consist of linear combinations of Gaussian functions. Let the regularization term be given by $r\left( {{{\left\| f \right\|}_H}} \right)$, where $r$ is a monotonically increasing function. Let the empirical risk take the general form of $\sum\limits_i {L\left( {{y_i},f\left( {{{\bf{x}}_i}} \right)} \right)} $, where the sum is over all data points in the training set. The objective function is therefore
| \[\sum\limits_i {L\left( {{y_i},f\left( {{{\bf{x}}_i}} \right)} \right)} + r\left( {{{\left\| {\Delta f} \right\|}_H}} \right)\] | [42] |
The representer theorem then states that the function that minimizes this objective function must take the form
| \[\hat f\left( {\bf{x}} \right) = \sum\limits_i {{c_i}k\left( {{{\bf{x}}_{\bf{i}}},{\bf{x}}} \right)} \] | [43] |
where the sum is over all elements of the training set.47, 48 Thus the problem of finding $\hat f$ is reduced to the problem of finding the coefficients ${c_i}$ that minimize the objective function.
If a squared loss function is used and $r\left( {{{\left\| {\Delta f} \right\|}_H}} \right) = \lambda \left\| {\Delta f} \right\|_H^2$ for some positive scalar $\lambda $, then it is straightforward to show that the objective function can be written as:
| \[\frac{1}{2}{\left\| {{\bf{y - Kc}}} \right\|^2} + \lambda {{\bf{c}}^{\bf{T}}}{\bf{Kc}}\] | [44] |
where ${\bf{K}}$ is a matrix in which ${K_{ij}} = k\left( {{{\bf{x}}_{\bf{i}}},{{\bf{x}}_{\bf{j}}}} \right)$ for some ${{\bf{x}}_{\bf{i}}}$ and ${{\bf{x}}_{\bf{j}}}$ in the training data, and ${\bf{c}}$ is a column vector in which the ${i^{th}}$ element is ${c_i}$. The unique solution to this problem is
| \[{\bf{\hat c}} = {\left( {{\bf{K}} + 2\lambda {\bf{I}}} \right)^{ - 1}}\] | [45] |
This approach is known as kernel ridge regression.49 It is similar to regularized linear least squares (equation [27]) with two major differences. The first is that it is no longer necessary to work in a hypothesis space of linear functions – this solution holds for any RKHS. The second is that the number of rows and columns in the matrix to be inverted is now equal to the number of elements in the training set, rather than the number of input variables. Thus although the calculations may take longer in situations in which there are a lot of training data, this approach can be used for a much wider variety of hypothesis spaces.
The flexibility and simplicity of kernel ridge regression has made it a popular tool in materials science. It has been used for a variety of ends, including the prediction of material properties from descriptors, development of model Hamiltonians, and generation of density functionals.
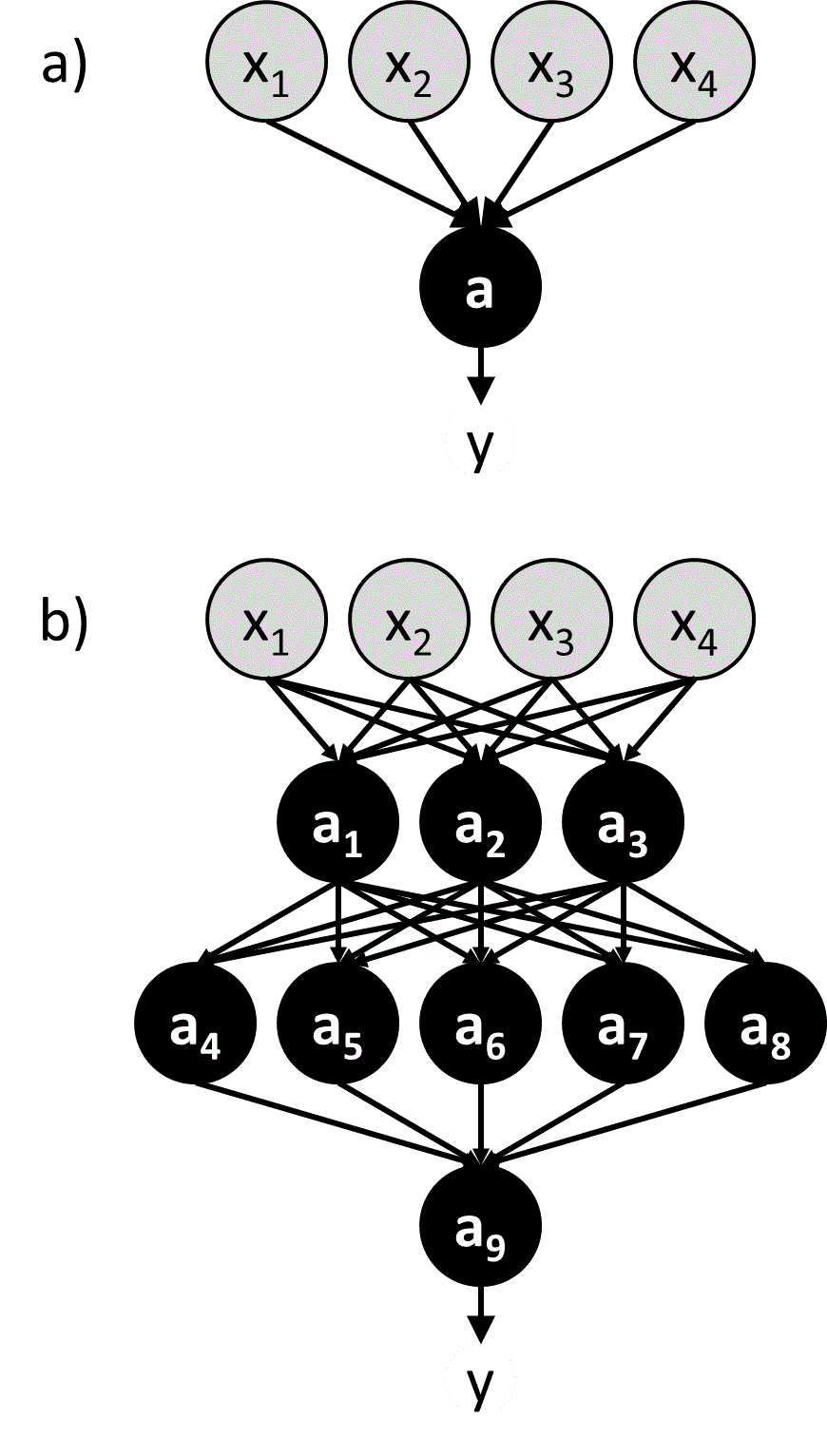
An intuitive and effective approach to machine learning is to mimic the biological brain. This is the idea behind a class of machine learning algorithms known as neural networks.50 In a neural network, artificial neurons (a.k.a. nodes) are linked together in a way that resembles the connections between neurons in the brain (Figure 5). The input values (${\bf{x}}$) are passed directly into a set of neurons that comprise the first layer of the neural network, and these neurons use activation functions to calculate output values that are then used as input values by the next set of neurons. This process proceeds throughout the network until reaching a neuron that produce the final output value ($y$). Some networks may be constructed to output multiple values.
Figure 5 a) A perceptron b) A multi-layer neural network containing many perceptron-like nodes. Nodes representing input variables (${x_1}$, ${x_2}$, …) are grey, and nodes with activation functions (${a_1}$, ${a_2}$, …) are black.
The hypothesis space in a neural network is defined by the topology of the connections between nodes and the parameterized activation functions used by the nodes. One of the simplest neural networks, consisting only of a single node, is known as a perceptron (Figure 5a).51 The activation function of a perceptron compares a weighted sum of the input values to a threshold value. If the weighted sum is larger than the threshold value, the perceptron produces “1” as the output value. If it is lower, the perceptron produces “0” as the output value. Mathematically, we write this activation function as:
| \[a\left( {\bf{x}} \right) = \left\{ {\begin{array}{*{20}{c}} 1 & {{\rm{if\hspace{1em} }}{\bf{w}} \cdot {\bf{x}} > b}\\ 0 & {{\rm{if\hspace{1em} }}{\bf{w}} \cdot {\bf{x}} \le b} \end{array}} \right.\] | [46] |
where $b$ is the threshold value and ${\bf{w}}$ is the vector of weights (Figure 6a). The perceptron is a linear classifier that is similar to a support vector machine, where the plane that separates two classes is determined by ${\bf{w}}$. The weights in a perceptron are typically optimized using a gradient descent algorithm to minimize the squared loss.
A perceptron is an example of a feed-forward network, in which there are no loops. More complicated feed-forward neural networks can be created by combining multiple perceptron-like nodes in a multi-layer network (Figure 5b). Such networks are sometimes referred to as multi-layer perceptrons. The optimization of the weights of a multi-layer perceptron is more complicated than that of single node, but it can be accomplished efficiently using a backpropagation algorithm that effectively minimizes the squared loss using gradient descent.52 However the backpropagation algorithm requires that the activation function is differentiable, which is not the case when using the function in equation [46]. To avoid this problem, in multi-layer neural networks the discontinuous step function used in equation [46] is replaced by a continuous sigmoid function such as a logistic function (Figure 6b). The use of continuous activation functions results in neural networks that can output a continuous range of output values, making neural networks valuable tools for regression as well as classification.53, 54
Figure 6 a) The discontinuous activation function in equation [46] b) A sigmoid activation function.
Multilayer perceptrons with sigmoid activation functions parameterized using backpropagation have been widely and successfully used for classification and regression. However there are a variety of alternatives to this approach. One alternative is recurrent neural networks, in which loops are allowed in the network, enabling the network to model dynamic processes. Different activation functions and optimization algorithms have also been developed to improve the performance of neural networks. A more extensive discussion of the different types of neural networks can be found in references 55 and 56. Across all types of neural networks, regularization is typically done by penalizing the complexity of the network as measured by factors such as the number of nodes in the network and the norm of the network weights.
Neural networks have had a long history of success in materials science and engineering, especially in the development of accurate interatomic potentials, and in the mapping of complex materials behavior (flow stress, fatigue behavior, microstructure, etc.) to materials processing parameters (heat treatment, deformation, cold working, etc.).
Decision trees are among the oldest approaches to machine learning, particularly for classification problems. Historically they have been among the most widely studied machine learning methods, and more comprehensive reviews of decision trees can be found in references 57-60. Within materials science, decision trees have been recently used to predict tribological properties (specifically, the coefficient of friction) of various materials based on easily accessible properties (or descriptors) of the materials and their constituents (e.g., melting point, Madelung constant, density, etc.).61 They have also been used to classify zeolite structures based on topological descriptors.62 Here we provide a brief overview of the idea behind decision trees and some common implementations.
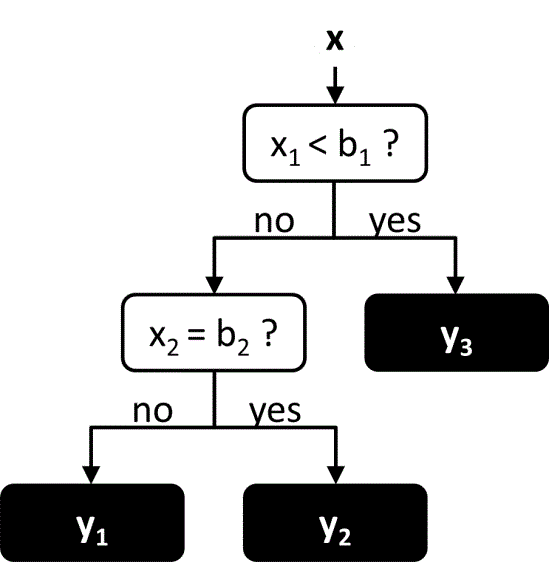
Decision trees are similar to neural networks in that the function is represented as a network of connected nodes. However in a decision tree, the network takes a hierarchical tree-like structure, in which each node may only have a single parent node (Figure 7). The evaluation of the function starts at the top-most parent node, known as the root node, and proceeds down through the tree until reaching a node with no children, known as the leaf node. At each node along the way there are multiple possible branches, each of which leads to a different child node. The choice of which branch to follow at each node is determined by value of one of the input variables. Thus the set of all input values determines the path through the tree, and the output value is determined by the leaf node that is reached at the end of the path. Decision trees are commonly used for classification, in which each leaf node corresponds to a different class. However they may also be used for regression, in which each leaf node corresponds to a different numerical value.
Figure 7 An example of a simple decision tree. The leaf nodes are in black.
There will generally be many different decision trees that are capable of reproducing the training data. The most efficient trees will be those that have, on average, the shortest path between the root and leaf nodes. Unfortunately the problem of finding such trees is NP-complete,63 meaning that it is unlikely that the globally optimal solution can be found using an algorithm that scales as a polynomial of the number of possible output values. Given the computational cost of finding a globally optimal solution, decision trees are commonly constructed using a greedy algorithm that finds a solution by making a locally optimal choice at each node. Some of the most successful algorithms are based on an approach known as Top-Down Induction of Decision Trees (TDIDT).64 In the TDIDT approach the tree is recursively built from the training data, starting at the root node. At each node an input variable is selected, and child nodes are created for each possible value of that variable. The training data are then divided into subsets based on the value of the input variable and passed to the appropriate child nodes. The process is then repeated at each child node, with each of the subsets divided and passed on to the next level of child nodes. If any of the subsets are empty, then a child node is not created, and if only one child node is created then the node becomes a leaf node. A common constraint is that there can be no path through the tree in which the same variable is evaluated more than once.
The TDIDT approach provides a general framework for creating decision trees, but it does not specify the order in which the input variables should be selected. A common approach for classification problems is to choose the input variable that produces subsets with the lowest average information entropy, where the information entropy for a subset is given by:
| \[ - N\sum\limits_i {{p_i}\ln {p_i}} \] | [47] |
In equation [47] the sum is over all classes in the subset, $N$ is the total number of elements in the subset, and ${p_i}$ is the fraction of elements in the subset that belong to the ${i^{th}}$ class. Information entropy is minimized for subsets that contain only one class and maximized for subsets that contain equal numbers of every class, and as a result this approach facilitates the rapid subdivision of the training data into subsets that are pure. A similar approach is to use the Gini Index in place of the information entropy,65 where the Gini Index is defined as:
| \[N\left( {1 - \sum\limits_i {{p_i}^2} } \right)\] | [48] |
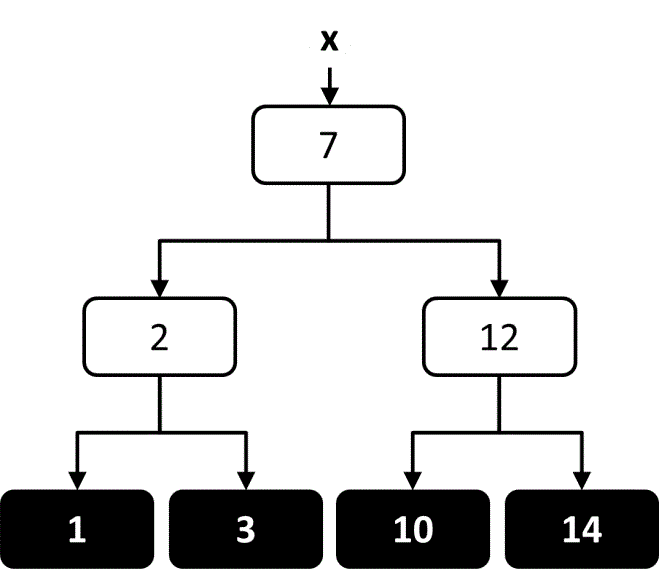
When using a decision tree for regression there is a continuous range of allowed output values, and it is common for every element in the training set to have a different output value. The objective of the decision tree is to provide an estimate of the output value that is close to the true output value. At each node in the tree, an estimate of the output value can be calculated based on the average of all output values in the leaf nodes below that node (Figure 8). The tree can then be constructed in a way that attempts to minimize the average estimation error along the path. One way to accomplish this within the TDIDT framework is to choose at each node the attribute that minimizes the average variance in output values within each of the subsets.65, 66
Figure 8 An illustration of how the output value could be estimated at each node in a regression decision tree trained on four output values.
There are two general strategies that can be used to improve the predictive accuracy of decision trees. The first is a regularization approach, in which the complexity of the tree is reduced by pruning, or removing, branches of the tree.65, 67, 68 The pruned branches are typically those that were poorly represented in the training data and / or are many layers from the root node. For regression, the pruned branches can be replaced by a function (e.g., using linear regression) that estimates the output values for the remaining set of input values. Resampling methods (described in the section on “Estimating the Prediction Error”) may be used to determine the optimal degree of pruning. An alternative approach to improving the prediction power is to generate ensembles of decision trees. For example, in the random forest approach, an ensemble of decision trees is created by introducing a stochastic element into the algorithm for constructing trees.69 The prediction is then based on the mode (for classification) or average (for regression) of predictions made by the members of the ensemble. Variations of this approach, known as ensemble learning, are described in the next section.
In ensemble learning, the function $\hat f$ is created by combining the outputs from an ensemble of different learning algorithms (e.g., by taking the average). This approach can be a simple and effective way to increase the size of the hypothesis space, and it often results in a function with greater predictive accuracy than any of the individual algorithms in the ensemble. It is particularly popular for classification problems.
Various approaches to ensemble learning are well-reviewed in references 70-72. Two of the most common classes of algorithms are bagging algorithms,73 in which the members of the ensemble are created by randomly resampling the training data, and boosting algorithms,74, 75 in which the training data is resampled in a way that assigns extra weight to input values for which the losses (described in the section on “The Empirical Risk”) are particularly high. The performance of some boosting algorithms can be adversely sensitive to random classification noise (i.e., erroneous classifications) in the training data.76
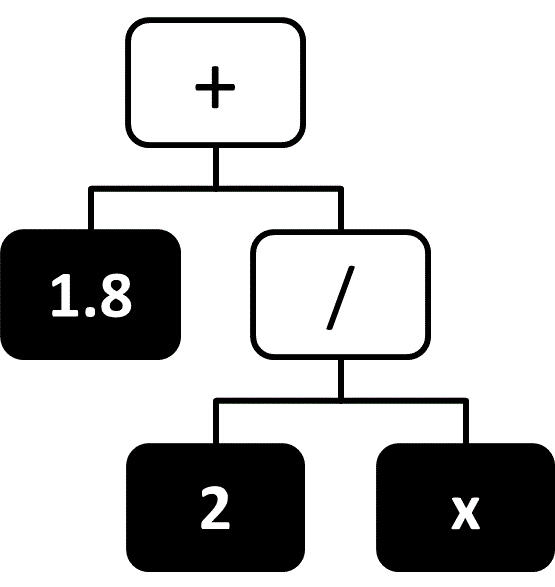
It is often desirable to express a function symbolically, as a simple combination of variables and basic mathematical operators. For example, the simple formula $F = ma$ is generally preferable to expressing force as a linear combination of many basis functions. The field of identifying such simple formulas that best predict the output values is known as symbolic regression. In symbolic regression the hypothesis space contains all symbolic formulas that combine the input variables with a set of mathematical operators, and the space is typically regularized in a way that favors simple formulas (e.g., formulas that contain fewer variables or operators). Functions are typically represented in a tree-like structure,77 where input variables and constant values are represented by the leaf nodes and the remaining nodes are mathematical operators or simple functions (e.g., trigonometric functions). An example of such a diagram is given in Figure 9.
Figure 9 A tree-like representation of the expression $1.8 + \frac{2}{x}$.
As with other supervised learning methods, symbolic regression is typically accomplished by searching through hypothesis space to find the formula that minimizes an objective function. A common way to do this is through genetic programming,78, 79 in which the search for the optimal function is performed using a genetic algorithm. In genetic programming a population of candidate formulas evolves in a way that mimics the process of natural selection, favoring the formulas that are most fit, i.e., formulas that produce the lowest values for the objective function. In a typical implementation, an initial population of candidate functions is created, and those that are least fit are discarded. The remaining functions are used to generate a new generation of functions by using crossover operations, in which features of the functions are combined to create “children”, and mutation operations, in which a feature of the function is randomly changed. Examples of crossover and mutation are shown in Figure 10. Repetition of this process results in a series of increasingly fit generations of functions.
Figure 10 a) An example of a crossover operation b) An example of a mutation operation.
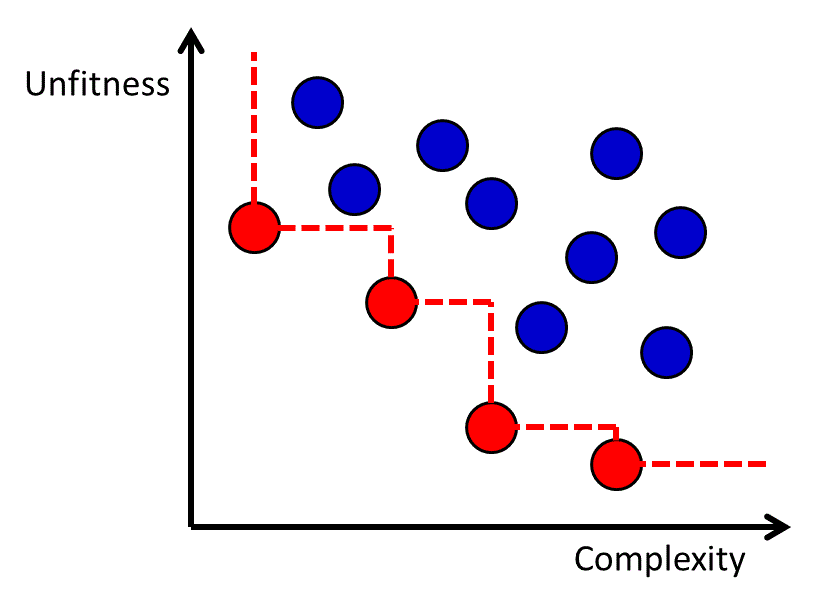
The genetic programming algorithm will generate a set of candidate functions with varying degrees of fitness and complexity. The complexity of the function may be measured by factors such as the number of nodes in the tree-like representation of the function, and it is common for complexity to be measured in a way that penalizes advanced operators such as acos more than simple operators like addition. Although it is possible to use a complexity-dependent regularization term in the objective function,78, 80 an alternative approach is to generate a Pareto frontier of the functions with respect to fitness and complexity.81 The Pareto frontier is defined as the set of all candidate functions for which there is no other known function that is both more fit and less complex. The Pareto frontier approach enables a transparent evaluation of the fitness-complexity trade-off in the population of functions generated by the genetic programming algorithm (Figure 11).
Figure 11 The Pareto frontier for a set of functions with different levels of fitness and complexity. Each dot represents a function, and the red dots (lower left dots connected by dashed line) are the ones on the Pareto Frontier.
In materials science and engineering, genetic programming has been used by several researchers to develop predictive models of the properties of cement and concrete,82-84 asphalt,85 and the effects of processing parameters on metal alloys.86-88 It has also recently been applied at the atomic scale, to determine the structural features of hydrogenated amorphous silicon that most strongly influence hole trap depths.89 A thorough review of genetic programming can be found in reference 90.
There are many comprehensive resources available for readers interested in learning more about machine learning algorithms and analysis. Two in particular are:
- T Hastie, J Friedman, and R Tibshirani, The Elements of Statistical Learning, Springer, 2009.
- CM Bishop, Pattern Recognition and Machine Learning, Springer, 2007.
Open source machine learning packages exist for all the algorithms described here. The open-source Weka software library is a collection of machine learning algorithms implemented in Java. The Python package scikit-learn has a library of methods with appropriate documentation. The commercial product MATLAB also has a library of methods as part of the toolboxes such as Statistics, Optimization, Neural Networks, Signal Processing, Image Processing, and Computer Vision. These methods come with extensive documentation including examples. For methods specific to image and video processing, the package OpenCV is extensive but may require background knowledge in machine learning. The commercial software package Eureqa provides a straightforward interface for genetic programming.
4. E. T. Jaynes, Physical Review, 106, 620-630 (1957). Information Theory and Statistical Mechanics.
5. Gideon Schwarz, The annals of statistics, 6, 461-464 (1978). Estimating the dimension of a model.
8. Reiner Horst, Introduction to global optimization, Springer, 2000.
9. Roger Fletcher, Practical methods of optimization, John Wiley & Sons, 2013.
16. Herman Chernoff, 586-602 (1953). Locally Optimal Designs for Estimating Parameters.
17. Abraham Wald, 134-140 (1943). On the Efficient Design of Statistical Investigations.
18. J. Kiefer and J. Wolfowitz, 271-294 (1959). Optimum Designs in Regression Problems.
22. Albert K Kurtz, Personnel Psychology, 1, 41-51 (1948). A research test of the Rorschach test.
41. Philip Wolfe, Econometrica, 27, 382-398 (1959). The Simplex Method for Quadratic Programming.
56. Simon Haykin, Neural networks: a comprehensive foundation, Prentice Hall PTR, 1998.
64. J. Ross Quinlan, Machine learning, 1, 81-106 (1986). Induction of decision trees.
69. Leo Breiman, Machine learning, 45, 5-32 (2001). Random forests.
71. Lior Rokach, Artificial Intelligence Review, 33, 1-39 (2010). Ensemble-based classifiers.
73. Leo Breiman, Machine learning, 24, 123-140 (1996). Bagging predictors.
74. Robert E Schapire, Machine learning, 5, 197-227 (1990). The strength of weak learnability.